Se você está interessado em calcular o crescimento de um investimento ao longo do tempo ou deseja saber o valor de uma dívida que acumula juros, sem precisar fazer cálculos manuais, a calculadora de juros compostos da meutudo é uma ferramenta muito útil. Veja Abaixo:
Aqui você também vai entender o conceito de juros compostos, como utilizar a calculadora para realizar esses cálculos de forma automática e compreender a fórmula por trás desse tipo de juros. Continue a leitura!
Como usar a calculadora de juros compostos online?
Utilizar a calculadora de juros compostos é muito prático, e ela pode ser usada para diversas combinações. Confira a seguir:
Para descobrir a taxa de juros aplicada
- Se a intenção é descobrir a taxa de juros aplicada na operação financeira, selecione o que você deseja calcular, nesse caso “taxa de juros”;
- Insira o capital, o qual é o valor inicial feito em um investimento ou outra operação financeira;
- Informe o prazo/tempo da operação, em meses ou anos;
- Por fim, insira o valor total final e aperte “Calcular”.
Para calcular o valor total ao final do período
- Selecione o que você deseja calcular, nesse caso “Valor total com juros”;
- Insira o capital, o qual é o valor inicial feito em um investimento ou outra operação financeira;
- Informe a taxa de juros anual ou mensal;
- Por fim, informe o prazo/tempo da operação, em meses ou anos, e aperte “Calcular”.
Para calcular o período necessário
- Para saber o tempo, selecione a opção “período/prazo”;
- Insira o capital, o qual é o valor inicial feito em um investimento ou outra operação financeira;
- Informe a taxa de juros, mensal ou anual;
- Por fim, insira o valor total final e aperte “Calcular”.
Como funcionam os juros compostos?
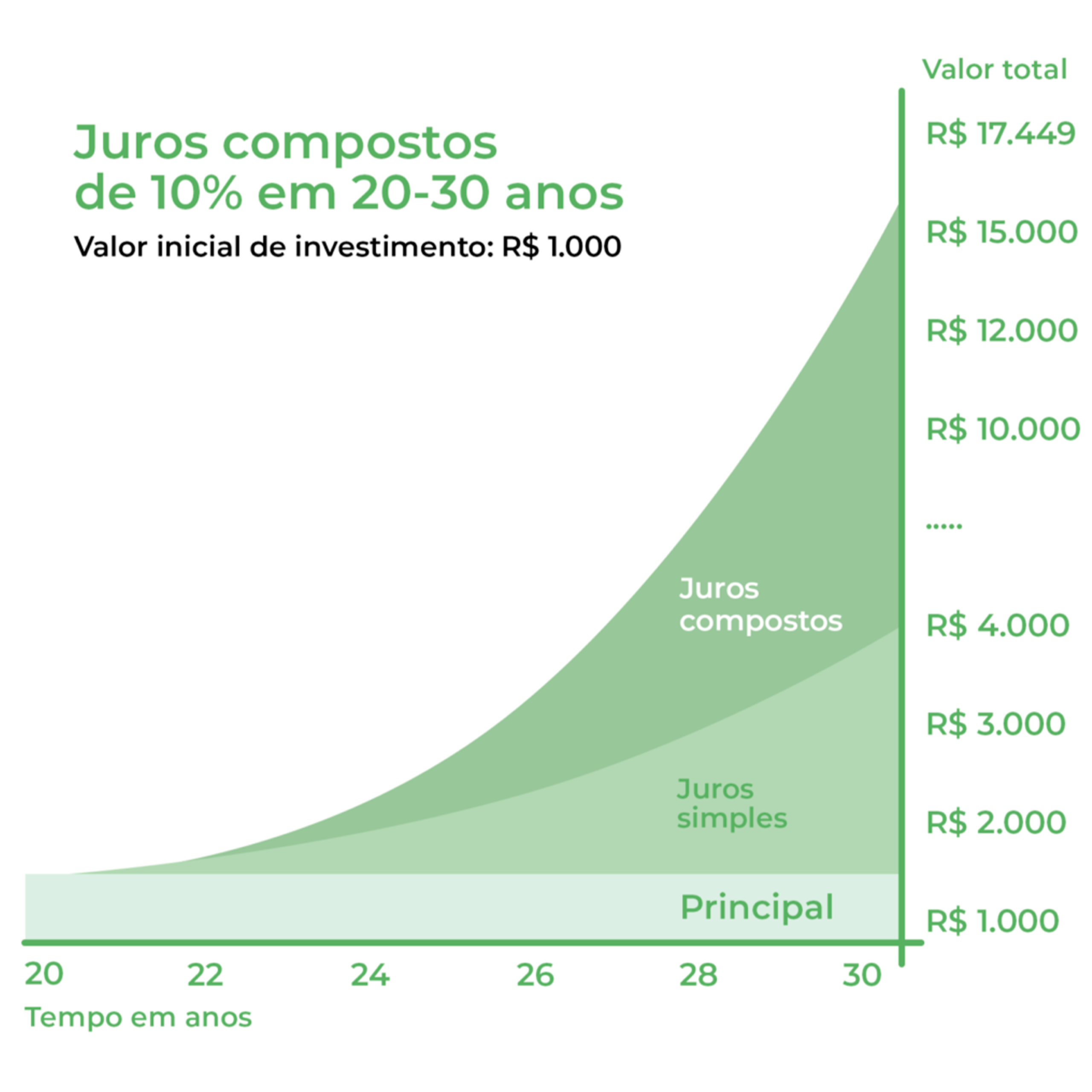
Os juros compostos, também conhecidos como juros sobre juros, são calculados tanto sobre o valor inicial quanto sobre os juros acumulados anteriormente.
Isso significa que, à medida que os juros compostos são aplicados em um investimento ou empréstimo, o valor total aumenta de forma exponencial ao longo do tempo.
Ao contrário dos juros simples, calculados apenas sobre o valor inicial, os juros compostos têm um efeito multiplicador. Isso os torna poderosos para o crescimento de investimentos ao longo do tempo.
Essa diferença de cálculo entre juros compostos e juros simples resulta em um crescimento mais acelerado do valor investido.
Enquanto os juros simples são calculados apenas com base no capital inicial, os juros compostos consideram tanto o capital inicial quanto os juros acumulados, o que leva a um aumento mais rápido do montante total.
Qual a fórmula dos juros compostos?
Para calcular os juros compostos, é preciso utilizar a seguinte fórmula:
M = C x (1 + i) ^ t
Onde:
- M é o montante total acumulado ao final do período desejado.
- C é valor de capital inicial investido.
- i é a taxa aplicada aos juros compostos.
- t é a quantidade de vezes que os juros serão acumulados ao longo do tempo
A taxa de juros e o número de períodos devem estar na mesma unidade, por exemplo, ao mês ou ao ano. Para usar a fórmula, a taxa de juros deve estar na forma decimal, ou seja, dividida por 100.
Por exemplo, suponhamos que Cristina tenha investido R$ 1.000,00 a uma taxa de 5% ao mês durante 6 meses, qual será o montante final (valor futuro)?
Substituindo na fórmula, temos:
M = 1.000 (1 + 0,05)6
M = 1.000 (1,05)6
M = 1.000 x 1,3401
M = 1.340,10
Portanto, o montante total será de R$ 1.340,10 e os juros serão de R$ 340,10 (R$ 1.340,10 – R$ 1.000,00).
Fórmula para descobrir a taxa de juros compostos
Para calcular a taxa de juros compostos, você pode seguir alguns passos simples. Vamos usar uma fórmula:
i = (M/C)^(1/t) – 1
Onde:
- i representa a taxa de juros compostos que queremos descobrir.
- M é o valor final do investimento.
- C é o valor inicial do investimento.
- t é o período em que o investimento foi feito.
Para exemplificar, suponhamos que Laura investiu R$ 5.000,00 e depois de 12 meses recebeu R$ 6.655,00.
Logo, para descobrir a taxa de juros compostos é preciso substituir os valores na fórmula:
i = (6.655,00/5.000,00)^(1/12) – 1
i = 1,0274 – 1
i = 0,0274
Portanto, a taxa de juros compostos foi de 2,74% ao mês. Esse é o valor que indica o crescimento do seu investimento a cada mês.
Fórmula para calcular o tempo de juros compostos
Para calcular o tempo necessário para atingir um determinado montante com juros compostos, é preciso seguir alguns passos simples utilizando a seguinte a fórmula:
t = log(M/C) / log(1 + i)
Onde:
- t representa o tempo que queremos descobrir;
- M é o montante final desejado;
- C é o capital inicial;
- i é a taxa de juros.
Se Maria investir R$ 1.000,00 a uma taxa de juros de 5% ao mês e quiser alcançar um montante de R$ 2.000,00, quanto tempo levará?
Agora, é preciso substituir os valores na fórmula:
t = log(2000/1000) / log(1 + 0,05)
t = log(2) / log(1,05)
t = 0,3010 / 0,0212
t = 14,21
Portanto, Maria precisará esperar aproximadamente 14 meses para alcançar o montante desejado. Esse é o tempo necessário para que o seu investimento dobre de valor com os juros compostos.
Como são calculados os juros compostos?
Seguindo o exemplo do tópico que mostra a fórmula utilizada para o cálculo dos juros compostos, Cristina tinha investido R$ 1.000,00 a uma taxa de 5% ao mês durante 6 meses e queria saber o montante final.
Agora veja como cada etapa é calculada:
É preciso transformar a taxa de 5% em decimal, e isso é feito ao dividir 5% por 100, que é 0,05.
M = 1.000 (1 + 0,05)6
Na etapa seguinte é necessário somar 1 + 0,05
M = 1.000 (1,05)6
Depois, é preciso aplicar a potência com o número de meses ou anos na soma realizada anteriormente
M = 1.000 x 1,3401
E por último é preciso multiplicar o resultado da potenciação pelo valor inicial
M = 1.340,10
Para fazer o cálculo de forma manual, é necessário ter uma calculadora que faz a potenciação. Normalmente a do celular tem essa opção.
Quando os juros compostos são mais utilizados?
Os juros compostos são muito utilizados em contratações de empréstimos consignados e investimentos, como renda fixa, fundos de investimento, financiamentos, cartão de crédito em atraso e outras operações financeiras.
Eles oferecem a oportunidade de aproveitar o poder do tempo e da acumulação dos juros para aumentar significativamente o valor do investimento ao longo do tempo.
Crédito
Para um empréstimo de R$ 10.000,00 com taxa de juros mensal de 1% por um período de 12 meses, a evolução é a seguinte:

Conforme a tabela apresentada, ao final de 12 meses, a dívida total é de R$11.268,25.
Como as parcelas dos empréstimos são fixas, ao chegar ao valor final contratado os bancos e instituições o divide em parcelas iguais.
Investimentos
Já em um investimento de R$ 10.000,00, com juros de 10% ao ano, durante 5 anos o aumento do valor final será conforme o da tabela:

O rendimento acontece a cada ano, mesmo que nenhum outro valor seja adicionado, porque os juros incidem sobre o capital e também sobre os juros anteriores.
Agora você já sabe os detalhes para calcular os juros compostos de forma manual e como
